摘要：区域机场群系统的协同发展已成为我国机场群发展的重要方向，然而面对区域机场群系统空域资源受限严重，航路点拥堵明显的客观环境下，机场群系统的航班时刻协同优化问题值得深入研究。本文以京津冀机场群为典型案例，以航班时刻调整量和延误量最小为目标，建立了机场群航班时刻优化模型，设计了实现算法。仿真结果表明，运用本文提出的优化模型和算法，京津冀机场多机场系统的航班延误得到明显降低。 

　　关键词：航空运输；航班时刻表优化；机场群系统；寻优算法 

　　一、概述 

　　空域拥堵和航班延误是制约多机场系统高质量发展的难题，为了破解这一难题，国内外众多学者从航班时刻优化、航班需求管理入手，按时间和空间、战略和战术、公平性和有效性等多维度开展研究，取得了一些进展。在航班时刻优化方面，2007年，徐进[4]对航空公司航班时刻频率和机型指派方法进行了研究，建立了一个基于旅客出行成本最小的航班时刻优化模型；2009年，Wang[2]等建立了多机场系统航班时刻优化数学模型，通过优化各航班的出发时间，减少机场拥堵与航班延误；2013年，刘佳[3]等在引入机场群概念的基础上，研究了枢纽因需求过量造成的空中交通流量拥堵问题，建立了航班降落机场选择的数学模型并设计了相关优化算法；同年，朱承元[5]等采用SIMMOD仿真建模和有约束限制的并行扰动随机近似优化算法（SPSA）相结合的方法，对机场群航班时刻进行了优化研究，确定各航班起飞的最优时刻；2018年，王倩[1]等建立了基于航空公司公平性的航班时刻优化模型,并设计了基于粒子群算法的布谷鸟搜索算法进行航班时刻表优化。在航班时刻需求管理方面，2010年，Czerny A I [6]运用时隙资源分配方法，采取拥堵收费、时隙拍卖等措施来管理航班时刻需求；2011年，刘方勤[7]等利用博弈理论对航空公司的决策进行分析建模，通过价格来调节需求，仿真实验验证了时隙拍卖能够降低拥挤空域的总延误成本，但没有考虑复杂多变的机场运行特性；2013年，吴刚[10]等基于旅客出行需求，将运输需求管理理论原理引入航班优化，减少机场群的航班延误。朱承元[11]等从机场群角度对多机场系统进行仿真优化，产生新的航班时刻，从而降低总延误时间。这类研究在一定程度上缓解了机场群的航班延误问题，但并未考虑航班时刻调整幅度与航班衔接的需求；2014年，Simaiakis I[9]对航班时刻表进行了优化，尽可能减少航空公司时刻需求和管理者时刻分配之间的差距，但没有考虑区域机场群的作用及航路点拥堵；2016年，杨新湦[8]等在满足机场延误水平的前提下，尽可能将航班时刻调整对航空公司和机场运行的影响降到最低，减少航班延误、提高放行正常率并降低航空公司和机场的损失。 

　　迄今为止，国内外学者在航班时刻优化与需求管理方面的大部分研究仅考虑了机场本身的容量约束，未能考虑终端区空域和航路拥堵，以及多机场联合运行产生的冲突，未能对机场群运行进行协同优化。因此，本文从空间和时间两个维度开展区域性多机场系统航班时刻协同优化研究，建立了机场群航班时刻协同优化模型，提出了一种基于飞行序列更新和时间滚动层的模拟退火算法，并以京津冀机场多机场系统为例，仿真验证了模型和算法的可行性。 

　　二、多机场系统航班时刻优化模型 

　　（一）符号定义 

　　航班集合，其中航班；机场集合，机场；航路点集合，航路点；时间窗集合，时间窗，也指机场运行时间，可分为若干个连续的时间窗，本文取15min为一个时间窗。机场的航班集合，过航路点的航班集合。为航班的调整量；为在机场航班的调整量；为机场的权重；和表示机场连续航班的最大和最小中转时间；和分别表示机场和航路点在时间窗的容量；和分别表示航班的最大调整量和总调整量；、、指与机场容量相关参数，分别是进离场服务率和容量。 

　　（二）航班时刻优化模型 

　　1．目标函数 

　　机场群航班时刻优化目标函数是航班时刻最大调整量、航班时刻调整总量、平均航班延误，以及航班延误最大值加权之和最小，即： 

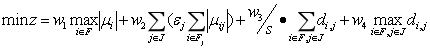　　     （2-1） 

　　其中，w1,w2,w3,w4为大于等于0、小于等于1的权值，且满足： 

　　                    （2-2） 

　　2.约束条件 

　　（1）满足唯一性限制。保证一个航班有且仅配置一个时刻。 

　　  （2-3） 

　　  （2-4） 

　　  （2-5） 

　　 （2-6） 

　　  （2-7） 

　　  （2-8） 

　　其中，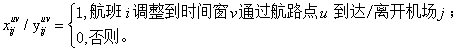 

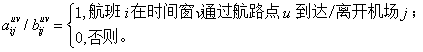
　　（2）需要满足连续性限制条件：连续性航班需满足相应机场最小及最大中转时间的要求，具有旅客连续性（联程）的航班需满足中转时间要求。 

　　           （2-9） 

　　           （2-10） 

　　其中，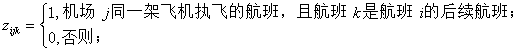  

　　（3）需要满足容量限制条件：各机场单位时间窗的容量限制、航路点（走廊口）的容量限制以及走廊口的唯一性。 

　　 （2-11） 

　　 , （2-12） 

　　 , （2-13） 

　　三、算法设计 

　　初始温度：temperature(l)=300+round(((0.98)^P)*100);      

　　同一温度下的寻优次数：iter=10+round((1-((0.95)^P))*P/4)*10; 

　　循环次数初始化：=1； 

　　while  temperature()>0.0001 

　　for i=1:iter 

　　通过蒙特卡洛法随机改变序列A，进而改变的值，得到新的航班序列temp_A，按FCFS计算X的方法，计算序列temp_A下的。 

　　判断新解是否可行，不可行则重复产生新解；最多重复次数设为30次，超过30次直接进入下一次循环，防止无可行解时限入死循环。 

　　计算增量=(X)，为多目标评价函数； 

　　If  <0   

　　     A=temp_A； (接受temp_A作为新的优化序列并进入下一次循环) 

　　X=；(接受作为新的当前解) 

　　=() ；（更新目标函数第次循环最优值） 

　　计算=()； 

　　If <0 

　　  opt_A=temp_A，(接受temp_A作为新的优化序列) 

　　  X_opt=，` 

　　=()，（更新全局最优可行解,下一次循环需要） 

　　    =()，（记录目标函数第次循环最优可行解, 下一次循环不需要） 

　　end 

　　elseif  exp(-/temperature())>rand() （否则根据Metropolis准则接受作为新的当前解。） 

　　            A=temp_A， 

　　            X=， 

　　=()，（非最优解，也不是第次循环最优值） 

　　end 

　　end (end for i=1:iter)  

　　=+1， 

　　temperature()=temperature(-1)*0.99; 

　　   if  temperature()<(temperature(1)*0.618) 

　　      temperature()= temperature(l)*0.6; 

　　   end 

　　end  (end while temperature()>0.0001) 

　　四、 案例分析与讨论 

　　京津冀多机场系统主要包括：北京首都国际机场(PEK)，天津滨海国际机场(TSN)，以及石家庄正定国际机场(SJW)。该地区的空域资源与大规模的航班需求冲突，因而不可避免地存在严重的空中拥堵。本文以京津冀多机场一天的飞行计划数据作为案例研究。本节介绍和讨论了改进优化算法和其在京津冀机场多机场系统案例研究中的应用效果。首先，说明了FCFS算法的结果；然后，本文说明了具有相等权重的模拟退火算法的结果（即w1=w2=w3=w4）；最后，我们说明了由不同权重得到的结果。 

　　（一）FCFS算法和具有相同权重的模拟退火算法 

　　表1 京津冀机场集团采用FCFS算法的结果 

　　表2 京津冀机场群延迟采用模拟退火算法的结果 

　　FCFS和具有相等权重的模拟退火方法的结果之间的比较表明：模拟退火算法的最大位移（min），平均位移（min），平均延误（min）最大延误（min）的值较小。 

　　（二）权重不同的模拟退火算法的结果 

　　表3 京津冀机场集团设置不同权重的结果 

　　从实验的结果及其比较来看，当模拟退火用于解决多目标优化航班时刻问题时，每个目标的权重对优化结果有很大影响。因为模拟退火算法具有启发式算法通有的不稳定性，即使使用合理的参数设置，仅运行一次模拟退火算法得到最优解的概率微乎其微。所以，最好并行使用多台计算机来计算不同权重的结果，以及使用本文所述的专家评估方法来选择最能满足各方利益的结果。 

　　五、结论 

　　由于空域资源有限，机场航班时刻表配置和运行在多机场系统中将会相互影响。因此，在多机场系统中，在不考虑其他机场的情况下，单机场航班时刻表的优化是次优的。为了解决这一问题，本文建立了机场群系统运行优化模型。为了提高航班时刻表的效率，减少航班时刻表的调整，本文对优化模型进行了改进并提出了优化算法。将优化算法应用于京津冀机场群，优化了航班时刻表的分配，有效控制调整后各时段的航班数量。综上所述，多机场系统的航班时刻优化模型和算法可以用来优化航班时刻表，从而缓解拥堵和延误问题。（作者：耿稀 民航局空管行业管理办公室 ） 

　　参考文献： 

　　[1]王倩, 翟文鹏. 基于航空公司公平性的航班时刻表优化研究[J]. 现代电子技术, 2018, 41(2):6-9. 

　　[2]Yanjun Wang, Minghua Hu, Dong Sui, Yong Tian. Departure Scheduling in a Multi-airport System [C]. Eighth USA/Europe Air Traffic Management Research and Development Seminar, 2009. 

　　[3]刘佳, 王莉莉. 基于机场群的航班选择机场模型分析研究[J]. 交通运输工程与信息学报, 2013(2):77-81. 

　　[4]徐进. 航空公司航班计划的优化方法研究[D]. 南京航空航天大学, 2007. 

　　[5]朱承元, 卫宏, 刁琳. 珠三角地区多机场系统航班时刻的仿真优化[J]. 计算机工程与应用, 2013, 49(4):236-239. 

　　[6]Czerny A I . Airport congestion management under uncertainty[J]. Transportation Research Part B: Methodological, 2010, 44(3):0-380. 

　　[7]刘方勤, 胡明华. 空域拥挤资源分配的拍卖方法研究和博弈均衡分析[J]. 南京航空航天大学学报（英文版）, 2011, 28(3):282-293. 

　　[8]杨新湦, 中国民航大学空中交通管理研究基地, 杨新湦, et al. 航班时刻资源优化配置与延误水平评估[J]. 河南科技大学学报（自然科学版）, 2016, 37(3):19-23. 

　　[9]Simaiakis I , Balakrishnan H . Dynamic Control of Airport Departures: Algorithm Development and Field Evaluation[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1):285-295. 

　　[10]吴刚, 夏洪山, 高强. 机场群运行方式下的航班时刻与频率优化模型[J]. 交通运输工程学报, 2013, 13(4):79-86. 

　　[11]朱承元, 卫宏, 刁琳. 珠三角地区多机场系统航班时刻的仿真优化[J]. 计算机工程与应用, 2013, 49(4):236-239.