航线网络上的延误传播分析及仿真研究
摘要:航班延误是世界航空运输业面临的一个重要问题,由于各种原因而引起的航班延误都给航空公司和旅客带来重大的经济损失。本文首先建立基于航线网络预期流的演化模型,以此为基础,进一步构建延误传播模型,并对延误特性进行了分析,结果表明本文所生成的航线网络的特征与实际网络运行特性相近,延误传播的特征也与实际网络中的传播特征相接近,对实际工作具有一定的指导意义。
文献[1-6]探索了复杂网络上的疾病或疫情传播的规律性,其中文[1]在SI模型基础上,构建了一个疾病传播模型,通过边权计算传播概率,并进行了仿真分析,结果表明,网络结构、边权及距离因素都对疫情传播有影响。文[2]研究了在基于欧拉距离偏好的小世界网络上的疫情传播和免疫策略,指出疫情传播由欧拉距离决定,提出了一个局部免疫策略和免疫半径。由于现有基于航班延误传播模型生成的网络与实际网络存在较大差距,因此需要进一步深入研究。本文首先建立了基于航线网络预期流的演化模型,以此为基础,进一步构建延误传播模型,并进行仿真分析。
一、建立基于航线网络预期流的演化模型
借鉴文[5]中的重力模型思想,建立网络演化模型。模型中目标函数为总的预期流,总成本为所需加入的边数。记网络节点集为![]() ,任意两节点间的预期流量为:
,任意两节点间的预期流量为:
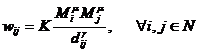 (1)
(1)
其中![]() ,
,![]() ,
,![]() 为未知参数,
为未知参数,![]() ,
,![]() 为节点
为节点![]() 和
和![]() 的适应度值,
的适应度值, ![]() 为节点
为节点![]() 和
和![]() 的欧氏距离。记
的欧氏距离。记![]() 为节点
为节点![]() 的最大吸引节点集,即
的最大吸引节点集,即![]() ,建立如下演化网络模型:
,建立如下演化网络模型:
Max![]()
s.t.![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
其中![]() 为需要构建的网络总边数。如果节点
为需要构建的网络总边数。如果节点![]() 和
和![]() 相连,
相连,![]() ,否则
,否则![]() 。模型的目标函数是使得总的预期流最大。当然目标函数也可替换为总的成本或收益,使得总成本最小或总收益最大。约束条件(2)使得网络边的总数(总成本)不超过给定的值。约束条件(3)保证节点至少与集合中的一个节点相连。(4)为变量取值约束。
。模型的目标函数是使得总的预期流最大。当然目标函数也可替换为总的成本或收益,使得总成本最小或总收益最大。约束条件(2)使得网络边的总数(总成本)不超过给定的值。约束条件(3)保证节点至少与集合中的一个节点相连。(4)为变量取值约束。
以2004年的相关经济数据和中国民航航线网络数据为基础,构建仿真航线网络。节点数为![]() ,边数为
,边数为![]() 。以2004年的第三产业产值为节点的适应度值。为获得参数
。以2004年的第三产业产值为节点的适应度值。为获得参数![]() ,
,![]() ,
,![]() 的近似值,选择2004年中国民航509条直达航线上的客流数据作为拟合对象,通过与实际数据拟合,得到
的近似值,选择2004年中国民航509条直达航线上的客流数据作为拟合对象,通过与实际数据拟合,得到![]() ,
,![]() ,
,![]() 。发现
。发现![]() ,这与文献[6]一致。生成的航线网络显示在图1中。
,这与文献[6]一致。生成的航线网络显示在图1中。
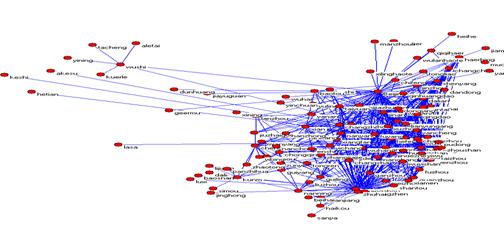
图1仿真航线网络
实际航线网络、模型仿真航线网络和文献[5]中航线网络的特征显示在表1中.
表1 网络特征对比
|
实际网络 |
本文生成的网络 |
文[103]生成的网络 |
|
|
层次性 |
有 |
有 |
有 |
|
度值最大的前四个城市 |
北京、上海、广州、深圳 |
北京、上海、广州、武汉 |
北京、上海、武汉、广州 |
|
网络平均路径长度 |
2.263 |
2.2656 |
2.302 |
|
pearson相关系数 |
-0.408 |
-0.4706 |
-0.401 |
|
beta1 |
-0.53 |
-0.4706 |
-0.46 |
|
beta2 |
-2.05 |
-3.3279 |
-2.3 |
|
kc |
20 |
19 |
22 |
由表1看到,与文[5]中的结果相比,参数![]() ,
,![]() ,
,![]() 新值的引入减少了距离因素的影响。节点度值最大的三个城市分别为北京、上海和广州,这与实际网络中的结论一致。
新值的引入减少了距离因素的影响。节点度值最大的三个城市分别为北京、上海和广州,这与实际网络中的结论一致。
二、建立航线网络延误传播模型
航班延误经常表征为实际出发(到达)时间比计划时间晚。发生在一个节点处的延误可通过边传递到其他节点。极端情形是一个节点处的延误可导致整个网络延误。下面将建立一个基于航线网络的延误传播模型。
设![]() 为节点集
为节点集![]() 中节点的数量,
中节点的数量,![]() 为延误节点数,
为延误节点数,![]() 为易感染(易延误)节点数,
为易感染(易延误)节点数,![]() 为恢复正常的节点数,则有
为恢复正常的节点数,则有![]() 。这里恢复成正常的节点可在延误传播过程中再次被感染。在航线网络中,两个节点间的延误传播主要与他们之间的流量、距离和节点度值因素有关。我们发现延误节点和易感节点之间流量越大、距离越短,易感节点被延误的可能性也越大,也发现延误节点的度值越小,延误传播的概率也越小,这表明具有小度值的延误节点有更多的时隙资源去缓解延误,因此延误对易感节点的影响将会比较小。记节点
。这里恢复成正常的节点可在延误传播过程中再次被感染。在航线网络中,两个节点间的延误传播主要与他们之间的流量、距离和节点度值因素有关。我们发现延误节点和易感节点之间流量越大、距离越短,易感节点被延误的可能性也越大,也发现延误节点的度值越小,延误传播的概率也越小,这表明具有小度值的延误节点有更多的时隙资源去缓解延误,因此延误对易感节点的影响将会比较小。记节点![]() 的度值为
的度值为![]() ,
,![]() 为节点
为节点![]() 的邻域节点集,
的邻域节点集,![]() 为从节点
为从节点![]() 至其邻域节点集
至其邻域节点集![]() 的最短距离,即
的最短距离,即![]() ,节点
,节点![]() 的点权记为
的点权记为![]() ,有
,有![]() ,从延误节点
,从延误节点![]() 至易感节点
至易感节点![]() 的延误传播率
的延误传播率![]() 可定义为
可定义为
![]() (5)
(5)
其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
记![]() 为时刻
为时刻![]() 集合
集合![]() 中的延误节点数,则易感节点
中的延误节点数,则易感节点![]() 延误的可能性为
延误的可能性为
![]() (6)
(6)
通常当延误发生时,管理者将会执行恢复策略,设![]() 为节点
为节点![]() 在时刻
在时刻![]() 的恢复能力,
的恢复能力, ![]() 越大,节点
越大,节点![]() 被延误的可能性越小。对于航线网络,在航班运行周期
被延误的可能性越小。对于航线网络,在航班运行周期![]() 内,航班为非均匀分布,并且每一节点处的旅客流必须运完。一般来说,节点处航班量越小越容易恢复,当
内,航班为非均匀分布,并且每一节点处的旅客流必须运完。一般来说,节点处航班量越小越容易恢复,当![]() 时恢复能力达到最大值1。因此节点
时恢复能力达到最大值1。因此节点![]() 在时刻
在时刻![]() 的恢复能力可定义为
的恢复能力可定义为
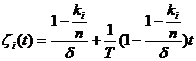 ( 7)
( 7)
其中![]() 。由方程(7)看到当
。由方程(7)看到当![]() 时,
时,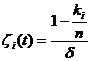 ;当
;当![]() 时
时![]() 。而且,如果节点
。而且,如果节点![]() 的度值很大, 当其他参数不变时,
的度值很大, 当其他参数不变时,![]() 将会很小。
将会很小。
三、延误传播过程仿真分析
在第一、二小节所生成的航线网络基础上,对延误传播过程进行仿真分析。通过仿真分析,有助于我们观察和分析初始延误在不同情形下引起的相继延误在网络中传播的范围和受延误影响的节点总数,也可对减弱延误影响或控制延误传播提供一些参考策略。下面各数据是1000次仿真结果的平均值。假定在初始时刻![]() ,有一个初始延误节点,该延误节点可随机选取或给定。每一时步,延误通过边的联系传播到该延误节点的邻域集中易感的节点,同时节点(机场)处管理者执行恢复策略。设
,有一个初始延误节点,该延误节点可随机选取或给定。每一时步,延误通过边的联系传播到该延误节点的邻域集中易感的节点,同时节点(机场)处管理者执行恢复策略。设![]() ,
,![]() ,
,![]() 。
。
(一)节点在有/无恢复能力情形下延误节点的数量分析
设![]() ,
,![]() ,初始延误节点在节点集
,初始延误节点在节点集![]() 中随机选择一个作为初始节点。下面分析当节点具有/不具有恢复能力情形下,网络中延误节点的数量的变化情况。仿真结果显示在图2中。
中随机选择一个作为初始节点。下面分析当节点具有/不具有恢复能力情形下,网络中延误节点的数量的变化情况。仿真结果显示在图2中。
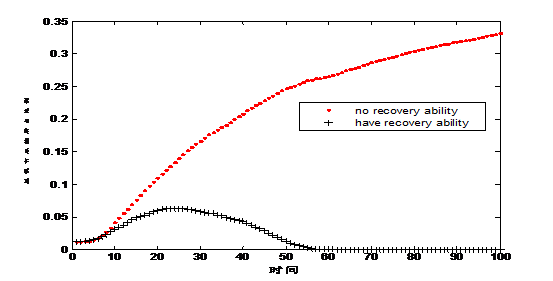
图2 在不同情形下网络中延误节点数
由图2可以看到,在节点不具有恢复能力的条件下,网络中延误节点的数量将会一直增加,当![]() 时,网络中将有32.47% 的节点被延误。然而,如果每一节点均存在恢复能力,网络中延误节点的数量先随着时间
时,网络中将有32.47% 的节点被延误。然而,如果每一节点均存在恢复能力,网络中延误节点的数量先随着时间![]() ,逐步增加,而后递减,当
,逐步增加,而后递减,当![]() 时达到最大值6.93%,当
时达到最大值6.93%,当![]() 时,网络中已经没有延误节点,即网络中不存在延误现象了。实际中,当延误发生时,管理者常常会迅速执行一些恢复策略,因此在下面的分析中,我们重点讨论节点具有恢复能力的条件下网络中的延误情形。
时,网络中已经没有延误节点,即网络中不存在延误现象了。实际中,当延误发生时,管理者常常会迅速执行一些恢复策略,因此在下面的分析中,我们重点讨论节点具有恢复能力的条件下网络中的延误情形。
(二)模型参数取不同组合值时延误节点数量和传播距离分析
初始延误节点随机选择,每一时步延误传播的距离定义为:延误节点集中节点距离初始延误节点最远的直线距离。延误的节点数量和延误传播的距离特征反映在图3,4和表2,3中。由图3可以看到对于每一种参数组合![]() 和
和![]() ,延误节点数量先增后减,最大延误节点数量越来越少,当
,延误节点数量先增后减,最大延误节点数量越来越少,当![]() 增加
增加![]() 递减时,网络用来消除延误所用的时间越来越短。网络中延误节点的数量变化特征显示在表2中。从图4看到每一种参数组合下,延误传播的距离先增加后减小。当
递减时,网络用来消除延误所用的时间越来越短。网络中延误节点的数量变化特征显示在表2中。从图4看到每一种参数组合下,延误传播的距离先增加后减小。当![]() 增加
增加![]() 递减时,延误传播的最远距离越来越短。延误传播距离的特征显示在表3中。
递减时,延误传播的最远距离越来越短。延误传播距离的特征显示在表3中。
表2![]() 、
、![]() 取不同参数值时,延误节点数
取不同参数值时,延误节点数
|
|
|
延误节点数量变化规律 |
最大延误节点数和达到最大的时刻 |
完全消除延误的初始时刻 |
|
0 |
1 |
先增后减 |
21.49%,t=19 |
t=88 |
|
0.2 |
0.8 |
先增后减 |
19.11%,t=25 |
t=83 |
|
0.8 |
0.2 |
先增后减 |
6.65%,t=22 |
t=64 |
|
1 |
0 |
先增后减 |
4.05%,t=22 |
t=60 |
表3![]() 、
、![]() 取不同参数值时,延误节点数
取不同参数值时,延误节点数
|
|
|
延误传播距离变化规律 |
时间[10,50]内传播距离 |
完全消除延误的初始时刻 |
|
0 |
1 |
先增后减 |
[720km,852km] |
t=88 |
|
0.2 |
0.8 |
先增后减 |
[638km,783km] |
t=83 |
|
0.8 |
0.2 |
先增后减 |
[198km,407km] |
t=64 |
|
1 |
0 |
先增后减 |
[115km,269km] |
t=60 |

图3![]() 、
、![]() 取不同参数值时,网络中延误节点数
取不同参数值时,网络中延误节点数
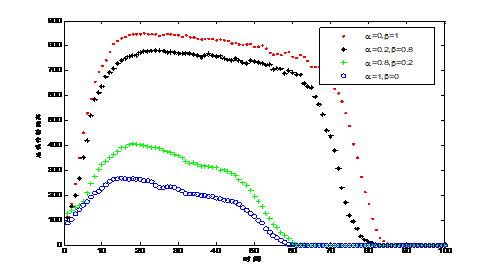
图4![]() 、
、![]() 取不同参数值时,网络延误传播的距离
取不同参数值时,网络延误传播的距离
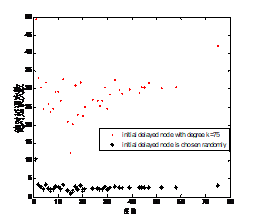
(三)初始延误节点具有不同度值时延误节点数量和传播距离分析
设![]() 、
、![]() 。假定初始延误分别发生在度值为
。假定初始延误分别发生在度值为![]() ,
,![]() ,
,![]() ,
,![]() 的节点处。延误节点数量和延误传播距离分别显示在图5,6中。由图5看到延误节点数量和延误数量达到峰值时的时刻不同。详细的数据特征反映在表4中。由表4看到当初始延误发生在度值较大的节点处,例如
的节点处。延误节点数量和延误传播距离分别显示在图5,6中。由图5看到延误节点数量和延误数量达到峰值时的时刻不同。详细的数据特征反映在表4中。由表4看到当初始延误发生在度值较大的节点处,例如![]() ,
,![]() ,度值越大,网络延误节点数量达到峰值的时刻越早,网络消除延误所用的时间也越长。由方程(5),看到 如果延误节点
,度值越大,网络延误节点数量达到峰值的时刻越早,网络消除延误所用的时间也越长。由方程(5),看到 如果延误节点![]() 的度值
的度值![]() 很大,传播率
很大,传播率![]() 也将很大,延误传播给它的邻域节点也越快。传播也将会发生在与延误节点相连的其它节点,故在短期内将会有很多节点被延误,网络消除延误所用时间也将越长。当初始延误发生在度值较小的节点处,例如
也将很大,延误传播给它的邻域节点也越快。传播也将会发生在与延误节点相连的其它节点,故在短期内将会有很多节点被延误,网络消除延误所用时间也将越长。当初始延误发生在度值较小的节点处,例如![]() ,
,![]() ,度值越小,网络延误节点数量达到峰值的时刻越早。这是因为
,度值越小,网络延误节点数量达到峰值的时刻越早。这是因为![]() 很小,在各节点具有恢复能力条件下,延误将不会迅速传播开去。因为延误节点数量很小,网络用来消除延误所用的时间也越短。
很小,在各节点具有恢复能力条件下,延误将不会迅速传播开去。因为延误节点数量很小,网络用来消除延误所用的时间也越短。
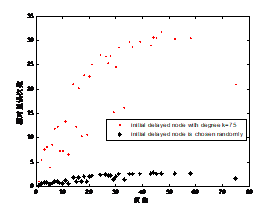
由图6看到当初始延误发生在度值不同的节点处时,延误传播的距离不同。详细的数据反映在表5中。由表4、5看到初始延误发生在度值越大的节点处时,延误节点的数量越多,延误传播的距离也越远。当初始延误发生在度值为![]() 的节点处时,在延误完全消除前的57.97%的时间内,延误将会影响到距离初始延误节点处[1824km,3154km]处的远距离节点,当初始延误发生在度值为
的节点处时,在延误完全消除前的57.97%的时间内,延误将会影响到距离初始延误节点处[1824km,3154km]处的远距离节点,当初始延误发生在度值为![]() 的节点处时,在网络消除延误前的63.49%的时间内,延误将会影响到距离初始延误节点[270km,577km]处的近距离节点。
的节点处时,在网络消除延误前的63.49%的时间内,延误将会影响到距离初始延误节点[270km,577km]处的近距离节点。
在实际的航线网络中,在度值大的节点处有许多航班。航班易受天气、航班密度等因素影响,因此航班经常容易延误。当延误发生在度值大的节点处时,尤其在网络的枢纽节点处时,与延误发生在度值小的节点处相比,延误发生在度值大的节点处时,其延误将会影响更多的节点和更远的传播距离。因此图5、6和表4、5所反映的特征与实际相一致。
表4 初始延误发生在不同度值节点处时,网络延误节点数
|
度 |
延误节点数量变化规律 |
最大延误节点数和达到最大的时刻 |
完全消除延误的初始时刻 |
|
75 |
先增后减 |
71.34%,t=22 |
t=69 |
|
31 |
先增后减 |
19.44%,t=26 |
t=65 |
|
20 |
先增后减 |
7.59%,t=24 |
t=63 |
|
5 |
递减 |
0.83%,t=1 |
t=60 |
表5 初始延误发生在不同度值节点处时,网络延误传播的距离
|
度 |
延误传播距离变化规律 |
最远传播距离和达到时刻 |
时间[10,50]内传播距离 |
完全消除延误的初始时刻 |
|
75 |
先增后减 |
3154km,t=20 |
[1824km,3154km] |
t=69 |
|
31 |
先增后减 |
1252km,t=22 |
[722km,1252km] |
t=65 |
|
20 |
先增后减 |
577km,t=20 |
[270km,577km] |
t=63 |
|
5 |
先增后减 |
37km,t=22 |
[12km,37km] |
t=60 |
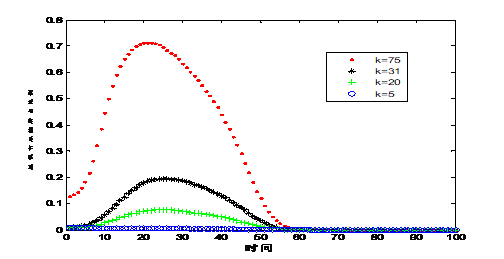
图5 初始延误发生在不同度值节点处时,网络延误节点数
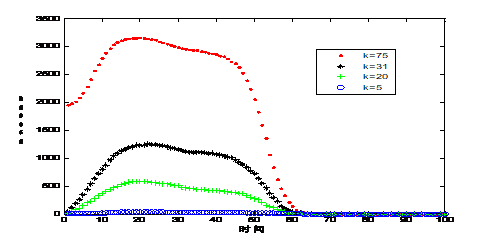
图6 初始延误发生在不同度值节点处时,网络延误传播的距离
(四)在航班运行周期内不同度值节点延误的次数
设![]() ,
,![]() 。记
。记![]() 为网络中节点的最大度值,在本文所生成的航线网络中
为网络中节点的最大度值,在本文所生成的航线网络中![]() 。在延误传播过程中哪些节点容易出现延误对于管理者来说很重要,管理者就可以在延误节点处有针对性地执行一些恢复策略。在下面的分析中,把有同样度值
。在延误传播过程中哪些节点容易出现延误对于管理者来说很重要,管理者就可以在延误节点处有针对性地执行一些恢复策略。在下面的分析中,把有同样度值![]() 的节点构成一个集合
的节点构成一个集合![]() 。集合
。集合![]() 中的节点具有同样的重要性。每一时步,
中的节点具有同样的重要性。每一时步,![]() 延误指该集合中的一个节点或多个节点出现延误。设
延误指该集合中的一个节点或多个节点出现延误。设![]() 时刻
时刻![]() 延误次数为0 。每一时步, 一旦
延误次数为0 。每一时步, 一旦![]() 出现延误,延误次数将加1,在航班运行周期内,将分析其出现的延误次数。记
出现延误,延误次数将加1,在航班运行周期内,将分析其出现的延误次数。记![]() 为集合
为集合![]() 中的节点数,
中的节点数,![]() ,
,![]() 分别为
分别为![]() 绝对、相对延误次数,则有
绝对、相对延误次数,则有![]() 。集合
。集合![]() 相对延误次数越多,表明在中国航线网络中具有度值为
相对延误次数越多,表明在中国航线网络中具有度值为![]() 的节点将对网络的运行起着重要作用。对于初始延误分别发生在度值为
的节点将对网络的运行起着重要作用。对于初始延误分别发生在度值为![]() 的节点处的节点随机选取,对节点的延误次数进行仿真分析。绝对和相对延误次数与度的关系显示在图7和8中。如果视
的节点处的节点随机选取,对节点的延误次数进行仿真分析。绝对和相对延误次数与度的关系显示在图7和8中。如果视![]() 为大度的节点,度
为大度的节点,度 ![]() 为小度节点,由图7看到小度值节点和大度值节点的延误次数在延误传播过程中都很大。在第一种情形下,即初始延误发生在度值
为小度节点,由图7看到小度值节点和大度值节点的延误次数在延误传播过程中都很大。在第一种情形下,即初始延误发生在度值![]() 的节点处时,不同度值节点延误次数要多于在第二种情形下的延误次数。在第一种情形下
的节点处时,不同度值节点延误次数要多于在第二种情形下的延误次数。在第一种情形下![]() ,
,![]() 的延误次数分别为49.4250,42.0170。由于网络度值为双段幂率分布,小度值节点的数量很多,因此出现较高的延误次数,而当初始延误节点发生在度值 为
的延误次数分别为49.4250,42.0170。由于网络度值为双段幂率分布,小度值节点的数量很多,因此出现较高的延误次数,而当初始延误节点发生在度值 为![]() 的节点处时,在航班运行周期内该节点需要较长时间去恢复正常,故度值为
的节点处时,在航班运行周期内该节点需要较长时间去恢复正常,故度值为![]() 的节点出现的延误次数也会比较多。节点的度值分布在[31,58]范围内时,平均延误次数为30次。当初始延误节点随机选取时,集合
的节点出现的延误次数也会比较多。节点的度值分布在[31,58]范围内时,平均延误次数为30次。当初始延误节点随机选取时,集合![]() ,
,![]() 出现的延误次数分别为10.5420,3.2710。度值分布在区间[31,58]范围内的节点平均延误次数为2.7次。由图8看到在两种情形下相对延误次数先递增后递减,峰值分别为
出现的延误次数分别为10.5420,3.2710。度值分布在区间[31,58]范围内的节点平均延误次数为2.7次。由图8看到在两种情形下相对延误次数先递增后递减,峰值分别为![]() ,31.7390 和
,31.7390 和![]() ,2.7650 。尽管在图7中集合
,2.7650 。尽管在图7中集合![]() ,
,![]() 的绝对延误次数最多,但是在图8中,看到他们的相对延误次数并不是最多。度值为
的绝对延误次数最多,但是在图8中,看到他们的相对延误次数并不是最多。度值为![]() ,
,![]() 的节点(在生成的中国航线网络中,代表杭州和济南),当延误发生时,这两个城市也应当作为预防和控制的重点城市。
的节点(在生成的中国航线网络中,代表杭州和济南),当延误发生时,这两个城市也应当作为预防和控制的重点城市。
|
图 7 绝对延误次数 |
图8 相对延误次数 |
四、小结
在本文中,我们建立了建立基于航线网络预期流的演化模型、建立航线网络延误传播模型,并在此基础上对延误传播过程进行了仿真,分析了延误节点数、延误传播距离和节点延误次数。结果表明由本文所生成的航线网络的特征与实际网络运行特性相近,延误传播的特征也与实际网络中的传播特征相接近,因此可以用本文所提出的理论和方法为航班延误预测和分析提供参考。(作者:吴小欢)
参考文献:
[1] Yan G, Zhou T, Wang J and et al. epidemic spreading in weighted scale free networks. Chinese Physics Letters,22(2):510-513.
[2] Guo W.-P, Li X, Wang X.-F.Epidemics and immunization on Euclidean distance preferred small-world networks. Physica A: Statistical Mechanics and its Applications, 2007,380: 684-690.
[3] Yoo J, Lee J.S, Kahng B.Disease spreading on fitness-rewired complex networks. Physica A: Statistical Mechanics and its Applications, 2011, 390(23): 4571-4576.
[4] Pastor-Satorras R, Vespignani A.Epidemic dynamics and endemic states in complex networks. Physical Review E, 2001,63(6):1-8.
[5] Qian J.-H, Han D.-D.A spatial weighted network model based on optimal expected traffic. Physica A: Statistical Mechanics and its Applications, 2009,88(19): 4248-4258.
[6] Bibb Latan´e J H L. Personality Social Psych. 1995,21:795.